By Dr. Amy
Jean Piaget stands as a pivotal figure in understanding child development, and his journey into this field is as fascinating as his contributions. Initially delving into the natural sciences, Piaget's career took an interesting turn towards psychoanalysis, sparking his deep interest in how humans learn and acquire knowledge. His theory of cognitive development, which tracks the growth of children from birth through adolescence, has been a game-changer in educational circles, particularly in teaching mathematics.
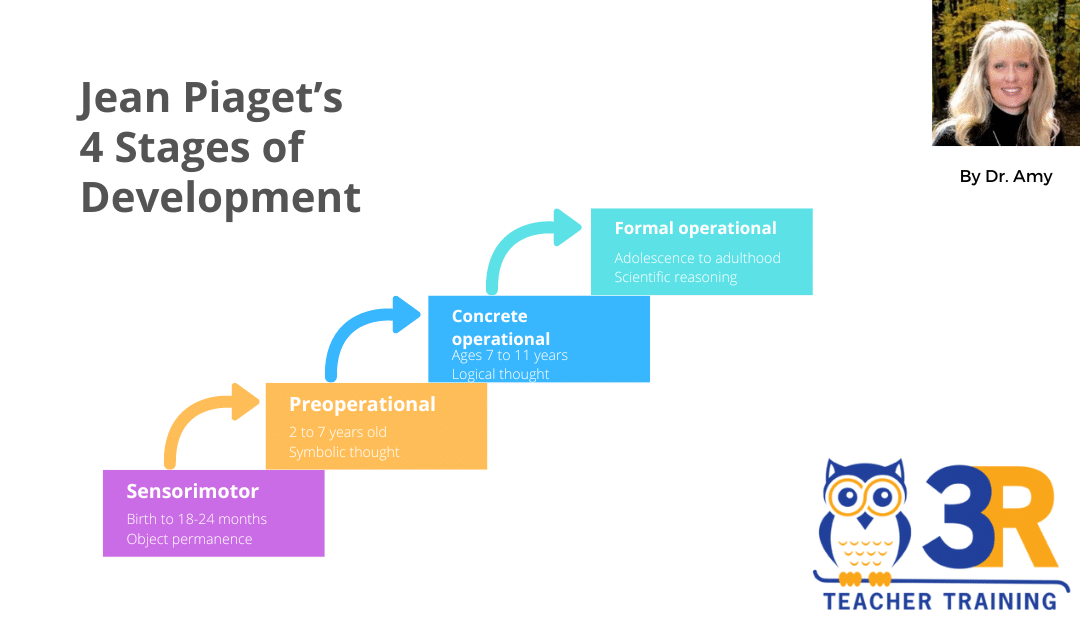
Piaget's theory is divided into four stages:
- Sensorimotor Stage (Birth to 2 years): This stage is all about learning through physical interaction with the world.
- Preoperational Stage (Approximately 2 through 7 years): Here, children start understanding symbols and engaging in imaginative play, but their thinking is quite centered on themselves, and they're still grasping the concept of time.
- Concrete Operational Stage (7 through early adolescence): During this period, kids develop a more logical approach to thinking about concrete events.
- Formal Operational Stage (Adolescence): This is where abstract thinking and hypothesis-driven reasoning come into play.
Now, let’s focus on the Preoperational Stage, which is especially relevant for children in early schooling (about ages 2 through first grade). During this stage, kids begin to realize that symbols (like words or numbers) can represent real-world objects. They’re full of imagination, think mostly about themselves, and are just starting to understand time. For educators, this is a golden opportunity to tailor mathematics teaching to align with these developmental milestones. For instance, you can use the idea that children are starting to connect symbols with objects to craft engaging math lessons.
Imagine you're planning a lesson to help children understand numbers. Here’s a friendly guide to get you started:
Learning Goal: Let's say your aim is for students to learn to count to 10 independently or recognize written numerals.
Materials You'll Need:
A set of toy cars
A bunch of apples
Several pieces of chalk
Number cards or a whiteboard to write numbers
Lesson Steps:
Introduction to Numbers: Start by showing the children a number, say ‘5’, and then count out five toy cars. This step connects the numeral ‘5’ (the symbol) to a tangible quantity (the cars).
Hands-On Practice: Give the children a chance to try it out. Ask them to pick a number card and then match the numeral with a corresponding number of apples. This reinforces their understanding of numbers as symbols for quantity.
Imaginative Play: Incorporate some make-believe scenarios. For example, “If we have 7 pieces of chalk, how many do we have if one is used by the teacher?” This not only helps in reinforcing the concept of number subtraction but also engages their imaginative minds.
Independent Counting: Encourage the children to count items or their toys up to 10. This activity ties back to the goal of them learning to count independently.
Number Recognition: Wrap up the lesson with a fun game where kids match written numerals to groups of objects.
Each step of this lesson plan is crafted with Piaget’s preoperational stage in mind. It acknowledges the children’s growing ability to understand symbols and their imaginative nature. By aligning your teaching strategy with Piaget’s theory, you not only make learning more effective but also a lot more fun for these young minds.
In conclusion, leveraging Piaget’s developmental stages, particularly the preoperational stage, can transform how we approach teaching mathematics to young children. It's all about aligning your teaching methods with their cognitive abilities, making learning an engaging and meaningful journey for the little learners.
Let's dive into Piaget's Concrete Operational Stage, a key phase in child development, particularly for those aged roughly 7 through early adolescence. During this stage, children develop the ability to think more logically about concrete objects and experiences. They can handle tasks involving multiple aspects of an object, order items by size or another attribute (seriation), and categorize objects effectively. To capitalize on these developmental milestones in the realm of mathematics education, hands-on learning and concrete examples are invaluable.
Lesson Plan: Understanding Multiplication and Place Value
Learning Objectives/Goals:
- Students will learn multiplication tables up to nine.
- Students will demonstrate an understanding of place value.
Materials Needed:
- Pattern blocks
- Math tiles
- Counter beads
Lesson Steps:
Introduction to Multiplication Tables: Using math tiles, demonstrate a multiplication example (e.g., 3×4). This step uses Piaget's concept of classification by grouping tiles into sets of three and showing four such groups.
- Hands-On Practice: Let students use counter beads to create their own multiplication sets. This step incorporates seriation as students arrange beads in rows and columns to represent multiplication facts.
- Exploring Place Value: Introduce place value using pattern blocks. For instance, a larger block could represent a ‘ten', and a smaller one a ‘one'. This is a concrete representation of number value, helping children understand the conservation of numbers despite changes in form.
- Independent Work: Encourage students to use math tiles to solve multiplication problems independently. This step reinforces their understanding of multiplication and allows them to apply the concept of seriation in a practical context.
- Group Activity: Have students work in groups to arrange pattern blocks according to place value in increasingly larger numbers. This activity not only reinforces the concept of place value but also encourages classification and grouping, critical aspects of Piaget's Concrete Operational Stage
- Review and Reflection: Conclude the lesson by reviewing key concepts and asking students to share what they learned. This helps reinforce the concepts and assess their understanding.
In addition to the above, it's vital to understand and incorporate elements of Piaget's Formal Operational Stage for older students. These adolescents are capable of abstract thinking, hypothesis testing, and applying concepts across different contexts. For such students, mathematics lessons can include complex word problems that require deductive reasoning, evaluating multiple pieces of information, and understanding algebraic concepts.
For example, a lesson on algebra might include:
- Materials: Algebraic expression cards, variable tiles.
- Lesson Steps: Start with simple expressions and gradually introduce more complex ones, linking each step to Piaget's concepts like hypothesis testing and abstract reasoning.
Finally, it’s important to remember that while Piaget’s stages offer a framework, they are not absolute. Each child's development is unique, and educators should remain flexible, adapting their teaching methods to meet the varied needs of their students. This approach ensures that all students, regardless of their developmental stage, receive an education that is both challenging and accessible.